Bakgrund⌗

Att få upp en funktionsgraf i Python med hjälp av matplotlib är inte svårt. Med lite googlande går det också att anpassa grafen på det som önskas. Ett problem för mig är att jag är en ganska sporadisk användare. Den tidsaspekten gör att jag hinner glömma bort syntax och detaljer mellan gångerna. Vidare har jag inte haft någon teori att bygga detaljerna på, uppgifterna som ska göras ofta varit för akuta för att jag ska ha hunnit sätta mig in i teorin. Det var upprinnelsen till att jag nu, när jag inte hade någon akut uppgift att göra, började sätta mig in i biblioteket mer “på riktigt”. Det ledde till att jag i alla fall har skrapat på ytan.

Exempel: Enklast möjliga plot⌗ 

import matplotlib.pyplot as plt
fig = plt.figure() # En figur skapas...
ax = fig.add_axes(0, 0, 1, 1) # I vilken ett diagram läggs in

# Punkterna förbinds
line = ax.plot([-2, -1, 0, 1, 2], [7, 6, 5, 4, 3])

# Punkterna plottas en och en
points = ax.plot([-2, -1, 0, 1, 2], [7, 6, 5, 4, 3], "o")

Här erhålls nu ett diagram:

Fig 1: Diagram med ett fåtal punkter

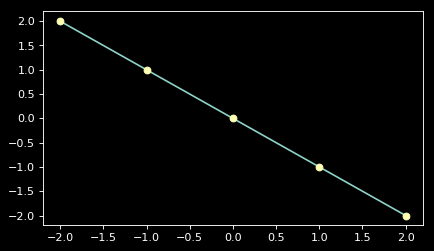
Fördelen med det här exemplet är att det blir tydligt vad som görs. Vi lägger till en figur, varpå diagrammet läggs i figuren, varpå grafen plottas i diagrammet. Nackdelen med exemplet är att det inte är så här som det brukar lösas; det är vanligt att vara mer generell på bekostnad av tydligheten.

Anatomin i matplotlib⌗

I det stora perspektivet är det viktigt att vara klar över anatomin och terminologin i matplotlib. Jag hittade en förklarande figur på deras webbplats.

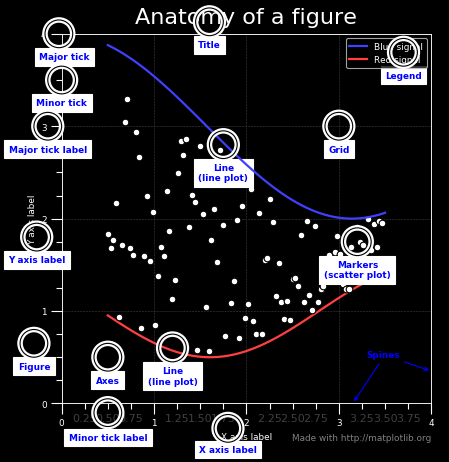
Anatomy of a figure
Fig. 2. Ingående element i en figur från matplotlib

Bilden finns på matplotlib:s FAQ-sida med källkod från denna sida (vilket gjorde att jag kunde modifiera den till mörk bakgrund).

För mig var det bl.a begreppen Axes och Axis som ställde till det tidigare, för att inte tala om Figure. I matplotlib:s objektorienterade design så gäller att Figure är klassen för hela bilden. Den måste finnas, men ofta görs inte så mycket med den. Storleken kan ställas in med hjälp av denna klass, liksom att den kan användas då en bild ska sparas. Men själva grafen och koordinatsystemet är en instans av klassen Axes. Med den görs det mesta som har med grafen att göra. En eller flera ´Axes´ läggs till i en Figure, som då alltså kan innehålla flera diagram. Klassen Axes ska inte förväxlas med metoden axis(), som har med själva koordinataxlarna att göra (som kan styras genom Axes), eller för den delen klassen Axis, som har funktioner för att styra allt som har med axlar att göra.

Exempel på funktionsgraf⌗

Som lärare i matematik är det framför allt en detalj i diagrammet i Fig. 1 som inte är till belåtenhet: koordinataxlarna. Diagrammt innesluts av en ram som också utgör koordinataxlarna. Men många mattelärare med mig önskar i sin undervisning koordinataxlar som skär varandra i origo.

Dessutom ska jag inte ha en linjär funktion denna gång, det innebär också att det kommer att behövas många fler koordinater än tidigare.

Låt oss plotta funktionen $y=3-e^{-x}$ i intervallet $-2\leq x\leq 5$

Fig 3: Funktionsgraf
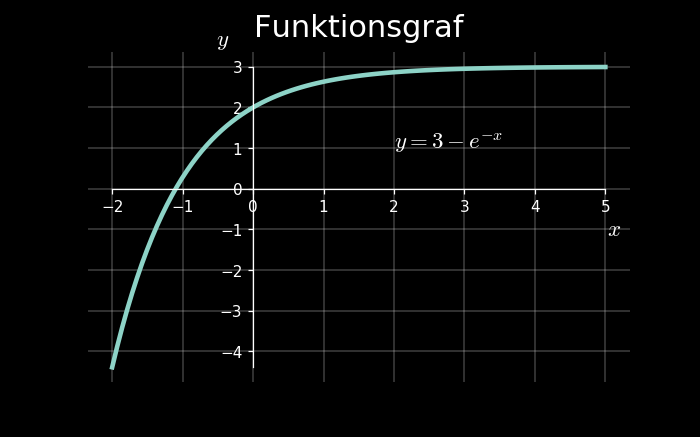
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["mathtext.fontset"] = "cm" # Ger ett bra typsnitt för formler
plt.style.use("dark_background") # "default" är den förinställda stilen

# Variabler som styr grafens storlek,
# upplösning och längd- breddförhållande.
width, dpi = (700, 110)
w = width / dpi
h = w*5/8

# Variablerna w och h är dimensioner i tum,
# därav "hacket" ovan där dessa beräknas utifrån
# antalet pixlar och pixeltätheten.
fig, ax = plt.subplots(figsize=(w, h), dpi=dpi)

# Koordinataxlarnas skärning med varandra
def setSpines():
    ax.spines['left'].set_position('zero')
    ax.spines['right'].set_color('none')
    ax.spines['bottom'].set_position('zero')
    ax.spines['top'].set_color('none')
    ax.spines['left'].set_smart_bounds(True)
    ax.spines['bottom'].set_smart_bounds(True)
    ax.xaxis.set_ticks_position('bottom')
    ax.yaxis.set_ticks_position('left')

# Ett rutnät
def setGrid():
    ax.grid(b=True, which='major', color='lightgrey',
            linestyle='-', linewidth=0.3)

# Själva funktionen som ska plottas
def f(x):
    return 3 - np.exp(-x)

# Några parametrar som styr utseendet på formlerna
# om inte "rotation" sätts kommer y-axelns etikett
# att vara vriden med 90°.
mathopts = { "rotation":0, "fontsize":15}
lineopts = {"linewidth":3}

# Skapar 100 värden mellan -2 och 5
x = np.linspace(-2, 5, 100)

# Axlar och rutnät ställs in
setSpines()
setGrid()

# Och här är själva plotten med etiketter
ax.plot(x, f(x), **lineopts)
ax.set_title("Funktionsgraf", fontsize=20, verticalalignment='bottom')
plt.xlabel("$x$", **mathopts) # Märkligt att etiketterna inte finns
plt.ylabel("$y$", **mathopts) # som en metod hos Axes...
ax.text(2, 1, "$y=3-e^{-x}$", **mathopts)
ax.xaxis.set_label_coords(0.97, 0.5)
ax.yaxis.set_label_coords(0.25, 1)

plt.show()
fig.savefig("funktionsgraf.png", transparent = False)

Ja, vi ser resultatet ovanför koden! Jag drog upp storleken och upplösningen på grafen en smula för att visa kvalitén. Likaså drog jag upp tjockleken på linjen. Det finns massor av inställningar som kan göras. Nedan finns några referenser som ingång.

Referenser⌗